Writing a Kakuro solver in CoffeeScript

A Kakuro is a Japanese number puzzle with the following rules:

• Each row and column must add up to the number directly above or to the left of it;
• You can only use the numbers one to nine;
• Each number in the row or column must be distinct.

I’ve written a Kakuro solver which you can play around with here: http://geotho.github.io/kakuro-solver/

If you are interested in seeing the solving code, you can do so here.

Below I describe some methods I tried to solve the Kakuros, some more successful that others.

Some things I tried that didn’t work well

Brute-force

Naively, a 12x10 kakuro has ~9^70 possible assignments. This is far too many to search exhaustively in a reasonable amount of time.

Constraint satisfaction algorithms

Kakuros, like Sudokus, are constraint satisfaction problems. The set of constraints one could create are firstly that numbers that share a row or column do not equal each other and that secondly the sum of the numbers in the row or column adds up to the total. The set of constraints therefore grows as O(n^2) where n is the number of cells in the Kakuro. CSP solving algorithms typicially rely on unary or binary constraints, whereas kakuro solving requires up to 9-ary constraints (e.g. A+B+C=6). One can rewrite any n-ary constraint into n x n! binary constraints but this factorial growth means CSP solvers are not particularly useful for this problem.

Solving kakuros

I’ve tried to incorporate some of the ways I solve Kakuros into the solver. The three techniques it uses to arrive at the correct value of a cell are:

1. Intersecting possible values of the cell from the row and the column.
2. Calculating values by adding rows and subtracting columns (and vice-versa).
3. Reducing possible values by contradiction until only one possible value remains.

Intersection of rows and columns

The only way to sum to 17 with two numbers is 9+8. The only way to sum to 16 with two numbers is 9+7. If we have a row of length two with a total of 17 intersecting a column of length two with a total of 16, there must be a nine in the cell that the row and column share.

Intersecting the possible values from the rows and the columns can reduce the size of the domain of the cell, potentially to a single value.

The intersection can be achieved by converting the row domain and the column domain to a bitmask and using a bitwise AND on them. I’m pretty sure this is a premature optimisation (and probably isn’t even an optimisation at all).

Adding rows and subtracting columns

Some values in kakuros can be uniquely determined using graph methods, such as the cell marked X in the image below.

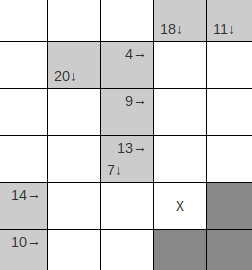
Considering a graph where all the vertices are cells in the Kakuro and each edge represents the relation “shares a row or column with”.

Then, to test whether a cell can be uniquely determined, remove its vertex from the graph and all the edges that connect to it. Then if the graph is no longer connected (can use a breadth-first search for this), the cell can be uniquely determined. Calculate its value by taking one of the now disconnected subgraphs (preferably the smaller one) and adding the value of its column or row, substracting all the values of its intersecting rows or columns and continuing recursively until exhausted. This is essentially using algebraic substitution.

Reducing possible values by contradiction

The objective of the two previous methods was to calculate the value of the cell. The objective of this method is to reduce the domain of possible values for a cell.

It works in a similar way to a proof by contradiction: first assume the cell has a particular value, then demonstrate that leaves a different cell with no possible remaining values. The implementation here gradually increases the depths to which it will look for a contradiction.

Thanks for reading! I hope this was useful. Please let me know if you have any questions or comments.