Analysing runtime of algorithms
In this post, I consider four different algorithms that solve the same problem.
The problem
Imagine a square 2D array that contains only zeroes and ones. Each row and column is sorted in ascending order. Count the number of zeroes.
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
I found this problem on CareerCup and was drawn initially to the uncertainty about the fastest possible algorithm.
The four algorithms I’m going to analyse are:
- linear counting
- binary search per row
- 2D binary search / quadtree
- saddleback search
Linear counting
The simplest of the four algorithms. Iterate over the array, incrementing a counter if we see a zero (note here and below I use booleans rather than 0s and 1s.)
func Count(arr [][]bool) int {
total := 0
for _, row := range arr {
for _, v := range row {
// if we hit a true, we can stop with this row
if v {
break
}
total++
}
}
return total
}
The runtime complexity of performing a linear count a N*N 2D array is O(N²), with O(1) memory requirement.
Binary search per row
To speed up our counting, we can perform a binary search on each row to find the last zero. If we know the index of the last zero, we know how many there are in each row.
func Count(arr [][]bool) int {
total := 0
zeroes := len(arr)
for _, row := range arr {
// Limit the row by the previous number of zeroes
zeroes := CountZeroes(row[:zeroes])
if zeroes == 0 {
break
}
total += zeroes
}
return total
}
func CountZeroes(row []bool) int {
if row[0] {
return 0
}
if !row[len(row)-1] {
return len(row)
}
hi := len(row)
lo := 0
for {
mid := (hi - 1 + lo) / 2
if !row[mid] {
if row[mid+1] {
return mid + 1
}
lo = mid + 1
continue
}
hi = mid
}
}
The runtime complexity of performing a binary search on a row of N numbers is O(logN). We have to do one binary search for each of the N rows, so the total complexity is O(NlogN), again with O(1) memory requirement.
Quadtree
A quadtree recursively divides a space into quadrants. Quadtrees can be used to count zeroes in the following way:
Pick the middle row in the array.
Find the last zero in this row. Call this point m.
Divide the array into four:
- The quadrant north-west of m is full only of zeroes. Add this to a total.
- The quadrant south-east of m is full only of ones. Ignore this completely.
- The north-east and south-west quadrants contain zeroes and ones. Recurse into each of these quadrants.
type point struct {x, y int}
func Count(arr [][]bool) int {
n := len(arr)
return countR(arr, point{0, 0}, point{n - 1, n - 1})
}
func countR(arr [][]bool, topLeft, bottomRight point) int {
if topLeft.x < 0 || topLeft.y < 0 {
return 0
}
if n := len(arr); bottomRight.x > n || bottomRight.y > n {
return 0
}
if bottomRight.x < topLeft.x || bottomRight.y < topLeft.y {
return 0
}
if topLeft == bottomRight {
if arr[topLeft.y][topLeft.x] {
return 0
}
return 1
}
if topLeft.y == bottomRight.y {
return CountZeroes(arr[topLeft.y][topLeft.x : bottomRight.x+1])
}
mid := (topLeft.y + bottomRight.y) / 2
midRow := arr[mid]
zeroes := CountZeroes(midRow) - 1
m := point{zeroes, mid}
return (m.x-topLeft.x+1)*(m.y-topLeft.y+1) +
countR(arr, point{topLeft.x, m.y + 1}, point{m.x, bottomRight.y}) +
countR(arr, point{m.x + 1, topLeft.y}, point{bottomRight.x, m.y - 1})
}
What is the computational complexity of this algorithm? The CareerCup discussion of this problem said O(logN), while I guessed O(log²N). Each recursion, you do logN work to find the midpoint and then do two smaller recursions on a problem a quarter of the size.
However, writing C(N²) for the complexity of an N² 2D array, solving the recursion C(N²) = logN + 2C(N²/4) yields a complexity of O(N). This is better than O(NlogN) but not quite as good as O(log²N) and far worse than O(logN).
A derivation is provided below:
{% raw %}
$$ \begin{aligned} C(N^2) &= \log_2 N + 2C\left(\frac{N^2}{4}\right) \ &= \log_2 N + 2\log_2 N/2 + 4C\left(\frac{N^2}{16}\right) \ &= \log_2 N + 2\log_2 N/2 + … + N\log_2 N/N \ &= \sum_{k=0}^{\log_2N} 2^k \log_2(N/2^k) \ &= \sum_{k=0}^{\log_2N} 2^k(\log_2N - \log_22^k \ &= \sum_{k=0}^{\log_2N} 2^k(\log_2N - k) \ &= \sum_{k=0}^{\log_2N} (2^k\log_2N - k2^k) \ &= \log_2N\sum_{k=0}^{\log_2N} 2^k - \sum_{k=0}^{\log_2N}k2^k \ &= \log_2N(2^{\log_2N + 1} - 1) - \sum_{k=0}^{\log_2N}k2^k \ &= \log_2N(2N - 1) - \sum_{k=0}^{\log_2N}k2^k \ &= \log_2N(2N - 1) - 2(2^{\log_2N}\log_2N - 2^{\log_2N} + 1) \ &= \log_2N(2N - 1) - 2(N\log_2N - N + 1) \ &= 2N -\log_2N - 2 \ &= O(N) \end{aligned} $$
{% endraw %}
What is the memory requirement? The stack grows exponentially (each recursion creates two more) but we are bound to O(logN) recursion depth, which gives a total stack memory requirement of O(N).
Note that neither tail-call optimisation nor an explicit stack would help to reduce our memory requirement.
Saddleback search
Can we do better? A far simpler O(N) algorithm is a Saddleback Search.
Start in the top right corner of the array. If we see a 1, move left. If we see a 0, add our current x position to a total, and then move down. Continue until we fall off the bottom or left of the array.
func Count(arr [][]bool) int {
x := len(arr) - 1
y := 0
total := 0
for x >= 0 && y < len(arr) {
if arr[y][x] {
x--
} else {
total += x + 1
y++
}
}
return total
}
This solution is much simpler and less error-prone than the quadtree counter. The complexity is again O(n) as the maximum number of steps we can take is 2n. It requires a small, constant amount of additional memory.
An empirical analysis of runtime
How well do our theoretical runtimes match reality? I used Go’s benchmarking facility to find out.
I precomputed many N² 2D array where the first row contained N 0s, the next contained N-1 0s and so on. A better set of benchmarks would also include various other patterns of 0s to get a more accurate picture of how each algorithm might perform on real world data. I created these arrays at intervals starting at 1x1 and ending at 100000x100000.
Using Go’s benchmarking facility means you don’t have to write logic to perform
multiple trials and average the results. This is handled for you, where quicker
methods (therefore those with a potentially higher variance) are subject to more
trials. When using go test -bench, remember to supply a RegEx as an argument
to bench, as by default no benchmarks are run. Use go test -bench . to run all
benchmarks. (I found this behaviour confusing as go test does not work this way).
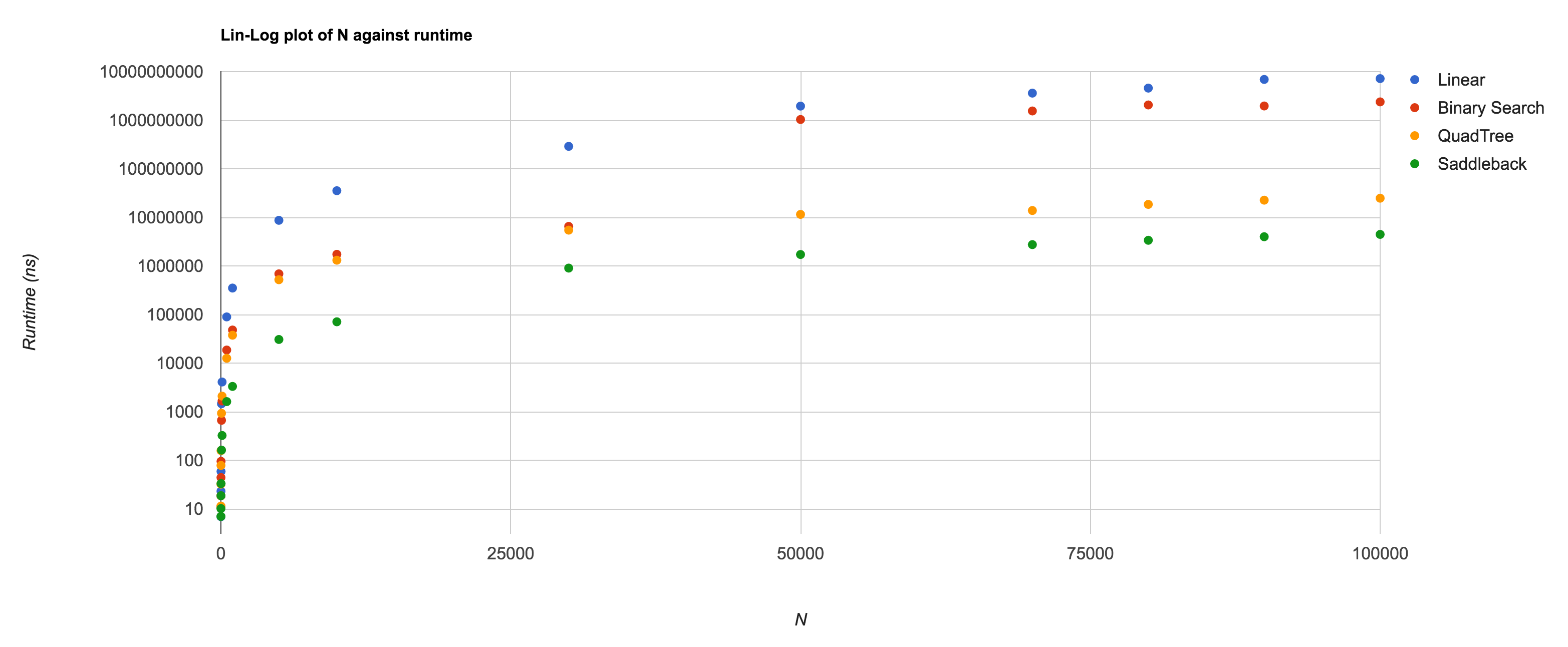
Here are the results:
| Array side length | Average Time taken (ns) |
| N | Linear | Binary Search | QuadTree | Saddleback |
|---|---|---|---|---|
| 1 | 6.96 | 11.2 | 11.5 | 7.06 |
| 2 | 10.8 | 18.7 | 32.5 | 10.2 |
| 5 | 23.3 | 44.4 | 79 | 18.8 |
| 10 | 59.3 | 95.7 | 159 | 33.4 |
| 50 | 1464 | 669 | 933 | 163 |
| 100 | 4107 | 1673 | 2103 | 326 |
| 500 | 89761 | 18681 | 12655 | 1623 |
| 1000 | 352023 | 48210 | 37724 | 3331 |
| 5000 | 8721353 | 690117 | 522126 | 30804 |
| 10000 | 35406766 | 1741224 | 1316930 | 71186 |
| 30000 | 289993371 | 6538812 | 5473949 | 906406 |
| 50000 | 1951491919 | 1034360290 | 11534336 | 1724967 |
| 70000 | 3608704183 | 1549914168 | 13875635 | 2755737 |
| 80000 | 4574500532 | 2060577730 | 18524247 | 3385933 |
| 90000 | 6899882267 | 1962937898 | 22651835 | 4002597 |
| 100000 | 7178311670 | 2383500531 | 24857549 | 4473402 |
And here are the results graphed on a lin-log plot of N against runtime:
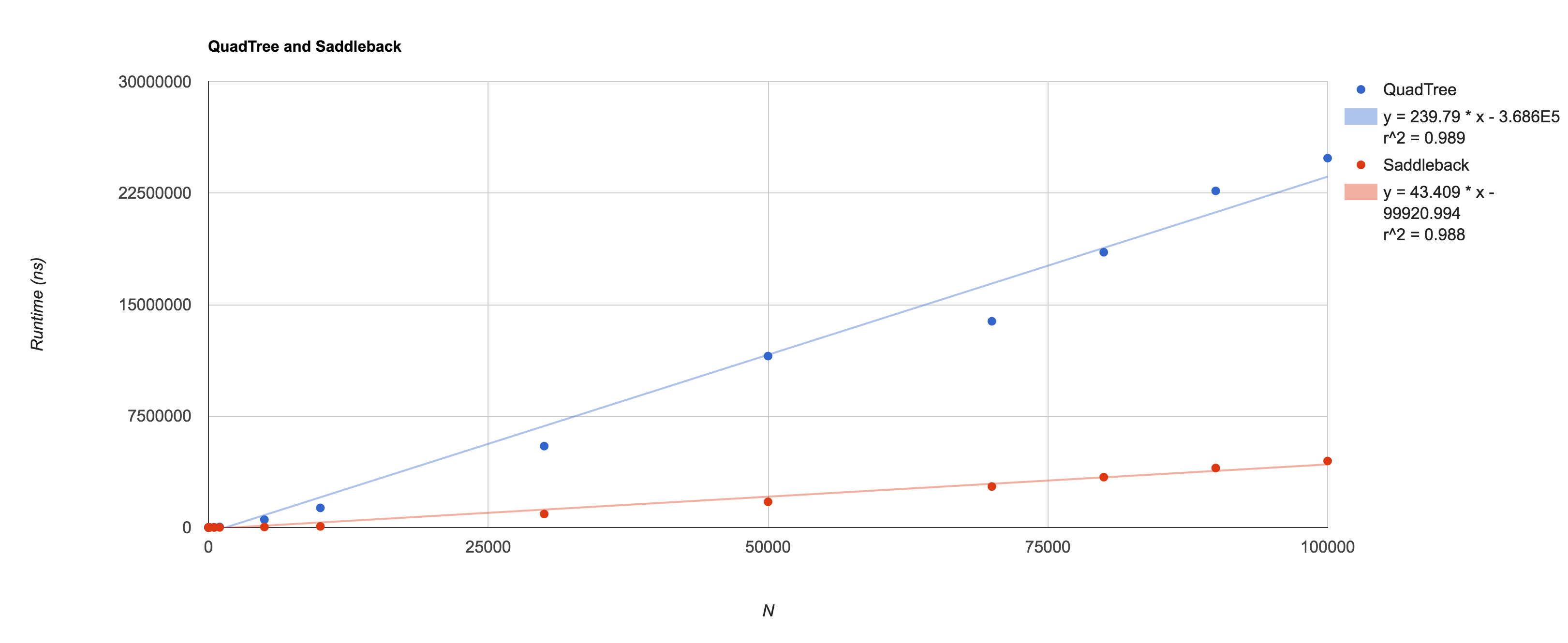
Finally, how can we tell whether our theoretical runtimes match up against our actual runtimes? Our runtimes shouldn’t grow faster than a linear multiple of our big-O past some size of input. Though totally unscientific, graphing our runtime against the big-O of our input size for the algorithm in question should give us some intuition as to whether our complexity is correct.
Here, I’ve plotted N against the runtimes of the quadtree and Saddleback algorithms:
You can view all the graphs and the data in this Google Doc.
Summary
I found it very satisfying that there are so many different algorithms for what is a reasonably simple problem, and doubtless there are a few more we have not yet explored (for example using a matrix multiplication, potentially on a GPU), and there are ways we could have made our other algorithms more efficient (e.g. by parallelising).
We’ve also shown that our theoretical run-times match approximately against empirical measurements, and the complexity of the quadtree-esque algorithm had a complexity of O(N) rather than O(log²N) as I’d originally guessed.
Thanks to my friends and colleagues who have had to listen to me ramble on about counting zeroes and ones in an array for far too long now, with not even a hint of “why would you ever want to do this.”