Recovering privacy zones on Strava
Strava is a website for tracking your athletic activity. I upload GPS recordings of my bike rides and it tells me how fast I am on particular segments of the ride.
Part of the fun of Strava is appearing on public leaderboards and seeing where you rank. This requires your activities to be public too, which means you potentially have to show your home or office location.
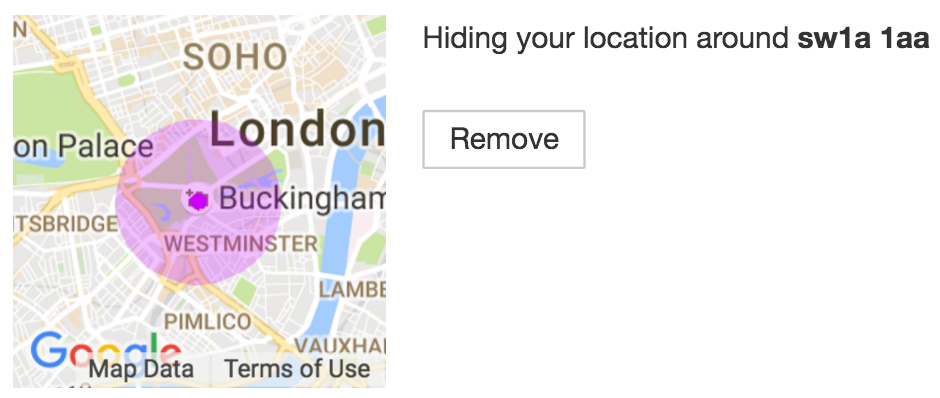
Not to worry – Strava has you covered. You can create privacy zones: “if your activity starts or ends within a 500m-1km radius of the address, the start and/or end of the activity will be hidden from other users.”
If I were the Queen, I could set up a privacy zone like so:
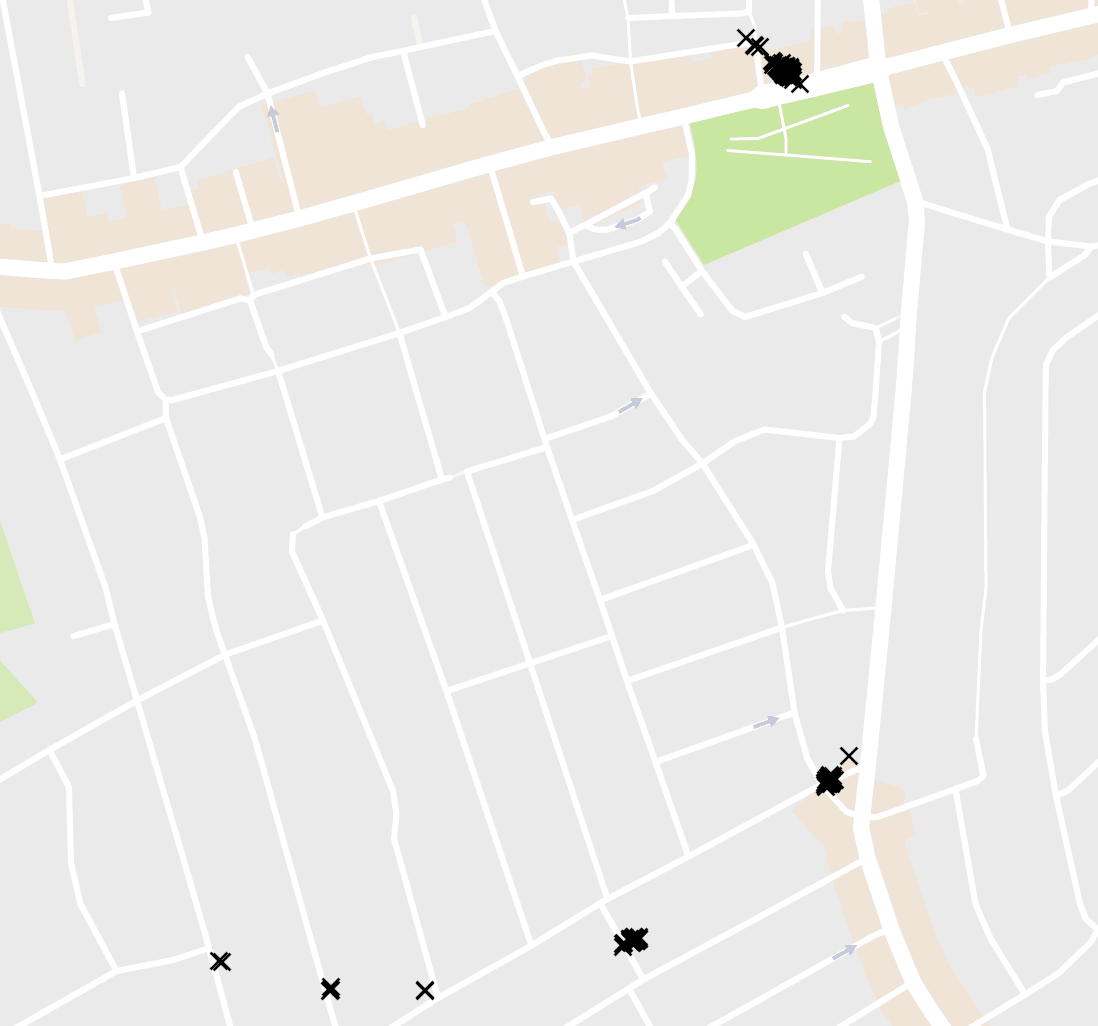
However, if, unlike the Queen, you go on lots of bike rides, the start and endpoints of all your rides might start to form a nice neat circle like this:
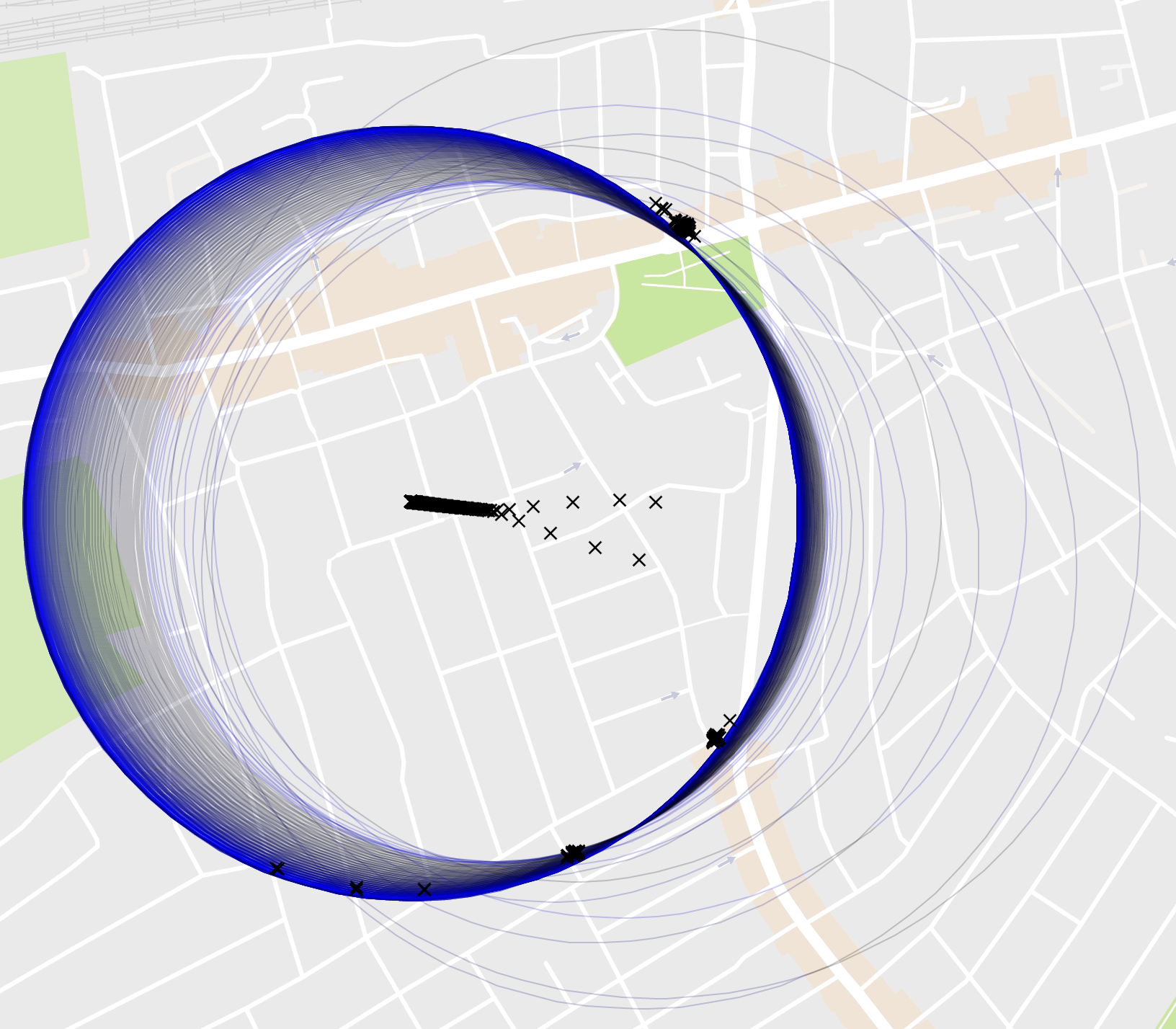
And a particularly enterprising privacy invader could use a gradient descent algorithm to fit a circle to your ride endpoints. The centre of the circle is then the centre of your “privacy” zone:
Some maths
I used the Euclidean distance rather than the great-circle distance (we are working with distances up to 1km). Writing \( \phi \) for latitude and \( \lambda \) for longitude, the distance D between two points is approximately:
$$ \begin{aligned} D(\lambda_1, \lambda_2, \phi_1, \phi_2) &\approx R\sqrt{(\lambda_2-\lambda_1)^2 + (\phi_2-\phi_1)^2\cos^2\frac{\lambda_2+\lambda_1}{2}} \end{aligned} $$Then, the partial derivatives w.r.t. one of the points are:
$$ \begin{aligned} \frac{\partial D}{\partial \lambda_1} &= R\frac{-2(\lambda_2-\lambda_1)-(\phi_2-\phi_1)^2\cos\frac{\lambda_2+\lambda_1}{2}\sin\frac{\lambda_2+\lambda_1}{2}}{\sqrt{(\lambda_2-\lambda_1)^2 + (\phi_2-\phi_1)^2\cos^2\frac{\lambda_2+\lambda_1}{2}}} \\ \\ \frac{\partial D}{\partial \phi_1} &= R\frac{-2(\phi_2-\phi_1)\cos\frac{\lambda_2+\lambda_1}{2}}{\sqrt{(\lambda_2-\lambda_1)^2 + (\phi_2-\phi_1)^2\cos^2\frac{\lambda_2+\lambda_1}{2}}} \end{aligned} $$We want to fit a circle with centre \( (\phi_c, \lambda_c) \) and radius \( r \) to our endpoints. Writing \( J(\phi_c, \lambda_c, r) \) for our cost function, we have for a set of \( m \) points \( p_i = (\lambda_i, \phi_i) \):
$$ \begin{aligned} J(\phi_c, \lambda_c, r) = \frac{1}{2m}\displaystyle\sum_{i=1}^m (D(\lambda_i, \lambda_c, \phi_i, \phi_c) - r)^2 \end{aligned} $$The partial derivatives of our cost function are therefore:
$$ \begin{aligned} \frac{\partial J}{\partial \phi_c} &= \frac{1}{m}\sum_{i=1}^m (D - r) \frac{\partial D}{\partial \phi_c} \\ \\ \frac{\partial J}{\partial \lambda_c} &= \frac{1}{m}\sum_{i=1}^m (D - r) \frac{\partial D}{\partial \lambda_c} \\ \\ \frac{\partial J}{\partial r} &= \frac{1}{m}\sum_{i=1}^m -(D - r) \end{aligned} $$And each gradient descent iteration becomes (for some rate parameter \( \alpha \)):
$$ \begin{aligned} \phi_c &:= \phi_c - \alpha\frac{\partial J}{\partial \phi_c} \\ \\ \lambda_c &:= \lambda_c - \alpha\frac{\partial J}{\partial \lambda_c} \\ \\ r &:= r - \alpha\frac{\partial J}{\partial r} \end{aligned} $$With some tweaking of the rate parameter, I managed to get the above with ~200 iterations.
I don’t consider this a glaring privacy invasion, for the following reasons:
- The privacy zone is centred on the postcode you type in, rather than your house. Thus the closest you could get is your street which could also be achieved by other means e.g. following you home.
- The privacy zone can include your home but not be centred on it (e.g. by entering the postcode of a neighbouring street).
- Slightly less plausible but you could also always leave the circle by the same route so as not to create many points on the circumference.